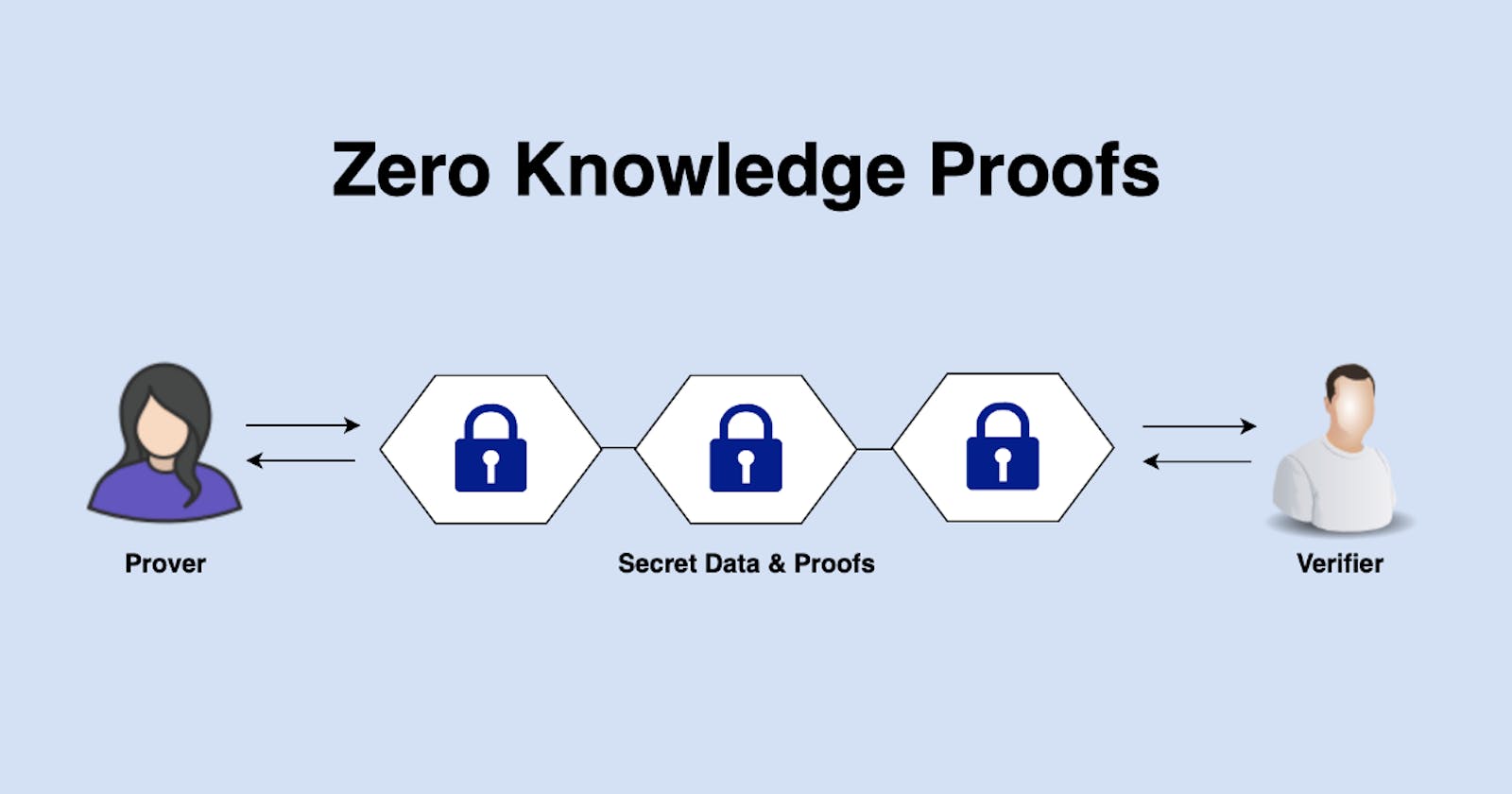
A zero-knowledge proof is a way of proving the validity of a statement without revealing the statement itself. This is done by using a proof that allows you to prove something to someone else, without giving them any information about what you have established.

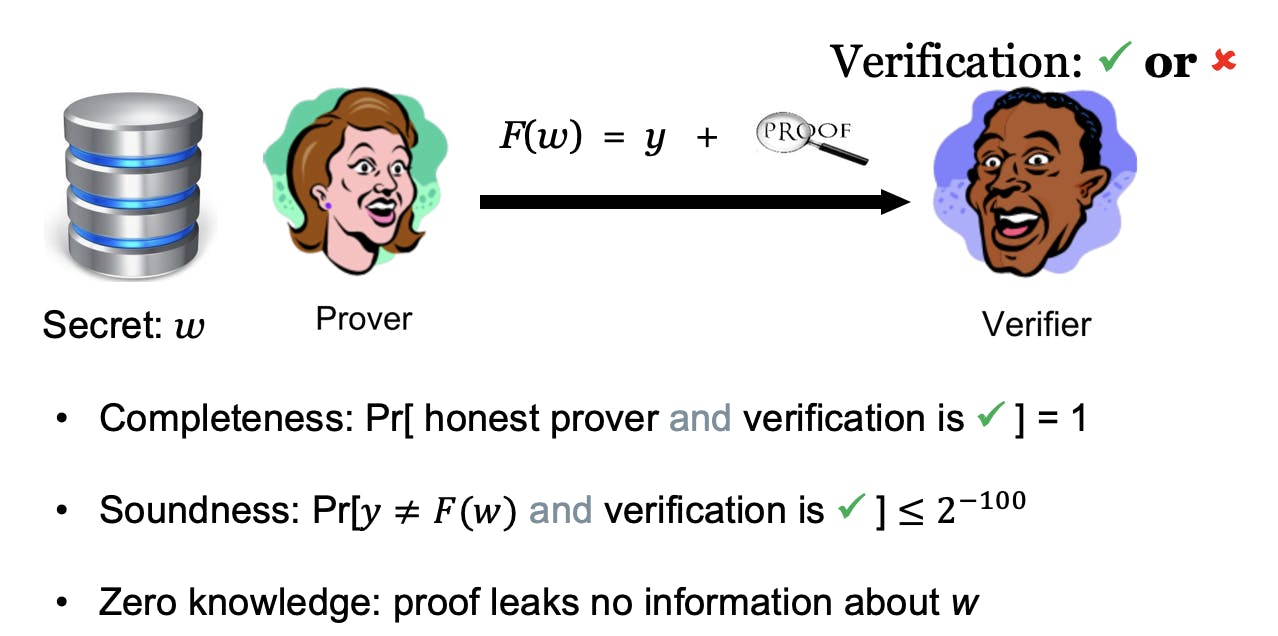
If I wanted to give my friend proof for some math problem they had been working on but didn't want to tell them what I had done, I could do so with zero-knowledge proof. I would prove that the solution was correct and then tell them it was right, but not how it was correct.

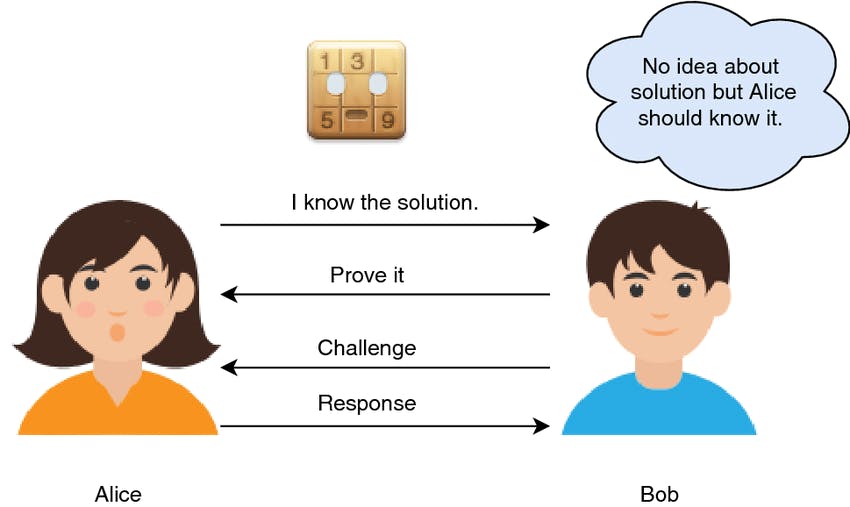
For example, there are two friends, Alice and Bob, out of whom Bob is color-blind. Alice has two balls and she needs to prove that both balls are of different colors.

Bob switches the balls randomly behind his back and shows them to Alice who has to tell if the balls are switched or not. If the balls are of the same color and Alice had given false information, the probability of her answering correctly is 50%. When the activity is repeated several times, the probability of Alice giving the correct answer with false information is significantly low.

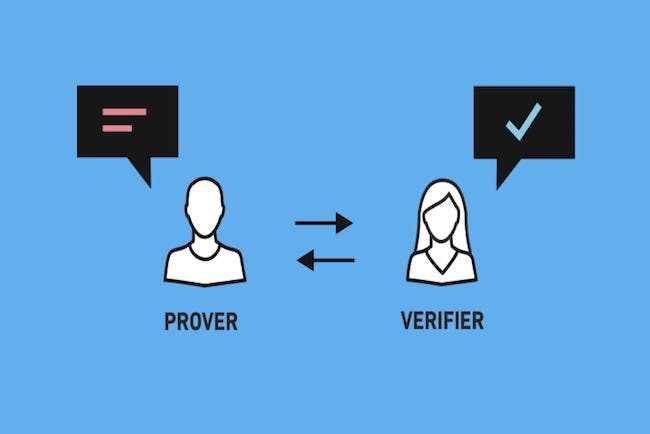
Here, Alice is the “prover” and Bob is the “verifier”. Colour is the absolute information or the algorithm to be executed, and it is proof of its soundness without revealing the information that is the color to the verifier.

I'd love to connect with you via Twitter | LinkedIn